Fachgruppe 0.0.1 - Petrinetze und verwandte Systemmodelle
Fachgruppe 0.0.1 - Petrinetze und verwandte Systemmodelle
Was sind Petrinetze?
Links
Petrinetze stellen einen Formalismus zur Beschreibung nebenläufiger Prozesse dar. Prof. Carl Adam Petri legte 1962 in seiner Dissertation "Kommunikation mit Automaten" die Grundlage für Petrinetze. Mehr als fünftausend Artikel haben sich seither mit diesem Thema beschäftigt.
Der Erfolg der Petrinetze gründet in ihrer einfachen und anschaulichen, zugleich aber auch formalen und ausdrucksstarken Natur und ihrem starken Bezug zur Praxis, der sich in der Vielzahl der durch Petrinetze beschreibbaren Systeme äußert. Zahlreiche computergestützte Werkzeuge stehen heute bereit, um die Entwicklung, Validierung und Verifikation von Petrinetzmodellen zu unterstützen.
Petrinetze sind gekennzeichnet durch eine strenge Trennung von passiven und aktiven Systemkomponenten, dargestellt durch passive und aktive Netzelemente, die Stellen bzw. Transitionen genannt werden. Die passiven Stellen (Elemente der Menge S, auch oft mit P für places bezeichnet) repräsentieren (lokale) Zustände des Systems, die während des Ablaufs eines Systems erfüllt sein können. Transitionen (Elemente der Menge T) stellen Aktionen oder Ereignisse dar, für deren Ausführung bzw. Eintreten bestimmte Zustände Voraussetzung sind und nach deren Auftreten bestimmte Zustände erreicht sind. In bezug auf Transitionen kann man die Zustände also auch als Bedingungen auffassen. Die Veränderung der Zustände des Systems durch eine Transition wird ihre Wirkung genannt und durch die sogenannte Flußrelation F codiert.
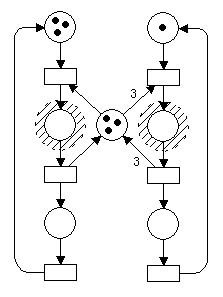Abbildung: Ein S/T-Netz für wechselseitigen Ausschluß
|
Ein weiterer Vorteil von Petrinetzen besteht in ihrer graphischen
Anschaulichkeit.
Die Stellen werden als Kreise, die Transitionen als Rechtecke und
die Flußrelation als Pfeile zwischen diesen dargestellt.
Ein Beispiel für ein Petrinetz in dieser Schreibweise enthält die nebenstehende Abbildung. Dieses Stellen/Transitions-Netz beschreibt den wechselseitigen Ausschluß zwischen drei lesenden und einem schreibenden Prozeß. Aufgrund der Markierung der mittleren Stelle und der entsprechenden Kantengewichtung ist es für alle erreichbaren Markierungen ausgeschlossen, daß sich der rechts dargestellte schreibende Prozeß und auch nur einer der links dargestellten lesenden Prozesse gleichzeitig im kritischen Abschnitt (in der Abbildung schraffiert hinterlegt) befinden. |
