Gedächtnisprotokoll FGI209-1

Die Klausur war wesentlich schwieriger als die im letztem Jahr (sofern man das an dem Gprot erkennen konnte) Man musste vorallem viele Definitionen können, und es kam vieles dran was so direkt nicht in den Übungsaufgaben besprochen wurde.

Auffallend war wieder die Personenkontrolle am Eingang.

Insgesamt gab es 192 Punkte zu erreichen

Aufgabe 1

Transitionssystem TS

<math>\rightarrow \overset{\overset{a}{\curvearrowleft}}{(s_0)} \rightarrow^b \overset{\overset{a}{\curvearrowleft}}{(s_1)} \rightarrow^b \overset{\overset{a}{\curvearrowleft}}{(s_2)} \rightarrow^b ...</math>

1. Formale Definition angeben:
   1. S=
   2. A=
   3. tr=
   4. <math>S^0</math>=
   5. <math>S^F</math>=
2. Wie ist die akzeptierte Sprache des Systems?
3. Geben sie einen endlichen Automaten an, der diese Sprache akzeptiert.
4. Geben sie die Omega-Sprache <math>L^\omega(TS)</math> an
5. Gegeben das Transitionssystem <math>TS_2 \rightarrow s_0' \overset{c}{\leftrightarrow} (s_1')</math> wobei <math>s_1'</math> Endzustand ist. Geben sie das Zustandsdiagramm des synchronen Transitionssystem <math>TS_1 \times TS_2</math> mit <math>Sync=\{(b,c)\}</math> und <math>\gamma(b,c)=d</math> an

Aufgabe 2

1. Geben sie die Definition einer Makierungsinvarianz an.
2. Geben sie die Definition einer Lebendigkeitsinvarianz an.
3. Geben sie die allgemeine Form eines Makierungsprädikates an.
4. Vervollständigen sie <math>m \rightarrow^t \Leftrightarrow \dots</math> wobei auf der rechten Seite ein Makierungsprädikat angegeben werden soll.

Aufgabe 3

1. Geben sie die formale Definition von Beschränktheit eines Netzes an.
2. Geben sie die formale Definition von struktureller Beschränktheit eines Netzes an.
3. Beweisen oder widerlegen sie die Behauptung:
   Wenn ein Netz beschränkt ist, und der Erreichbarkeitsgraph zwei oder mehr strenge Zusammenhangskomponenten besitzt, dann ist das Netz nicht reversibel.
4. Ändert es etwas, wenn das Netz unbeschränkt ist?

Aufgabe 4

Hier gab es allgemeine Fragen zu einem Erreichbarkeitsgraphen <math>RG( \mathcal N)</math> und einem Überdeckungsgraphen <math>G(\mathcal N)</math> eines Netzes. Auch hier Ja/Nein Kreuze und begründen.

1. Wenn das Netz beschränkt ist, ist dann <math>RG(\mathcal N)</math> endlich?
2. Wenn das Netz unbeschränkt ist, ist dann <math>RG(\mathcal N)</math> unendlich?
3. Wenn das Netz unbeschränkt ist, gibt es dann zwingend den Knoten <math>(\omega,\omega,\dots,\omega)</math> in <math>G(\mathcal N)</math>?
4. Wenn ein Platz <math>p_i</math> unbeschränkt ist, gilt dann <math>(x_0,x_1, \dots,\omega,...,x_n)</math>. (<math>\omega</math> ist an der Stelle <math>i</math>) für jeden Knoten im Überdeckungsgraphen <math>G(\mathcal N)</math>?
5. Hier war ein Petrinetz gegeben, und es sollte der Überdeckungsgraph gezeichnet werden. Dann sollte die Menge der unbeschränkten Plätze angegeben werden.

Aufgabe 5

(ich glaube man musste bei den Fragen Ja/Nein ankreuzen und begründen.)

1. Ist es entscheidbar ob ein P/T Netz beschränkt ist?
2. Ist es entscheidbar ob ein P/T Netz k-beschränkt ist?
3. Ist die Erreichbarkeit für CPN entscheidbar?
4. Gegeben ist ein P/T Netz mit <math>|P|</math> Plätzen und <math>|T|</math> Transitionen. Wir wissen, dass es <math>k</math>-beschränkt ist. Geben sie eine obere Abschätzung für die Anzahl der Knoten an, die der Erreichbarkeitsgraph hat!

Aufgabe 6

Gegeben war ein CPN.

1. zeichne den Erreichbarkeitsgraphen
2. Ist die Makierung (1'1 , <math> \emptyset </math>, 1'false) erreichbar?
3. Gilt <math>\forall p \in P : \forall m \in R(N) : \mid m(p)\mid \leq 1</math> ?

Aufgabe 7

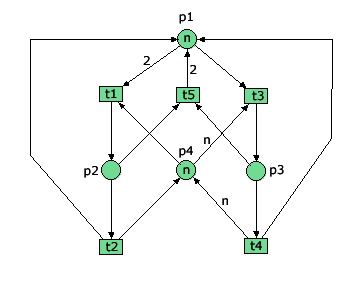
Gegeben war das Netz

und die invarianten

1. <math>\forall m \in R(m_ {0} : m(p1) + m(p2) + m(p3) = n)</math>
2. <math>\forall m \in R(m_ {0} : m(p2) + nm(p2) + m(p4) = n)</math>

Aufgabe 8

Hier gab es viele Punkte zur Prozessalgebra.

<math>t1 = d((ac + b)e) + d((b + c)a) + ba</math>

<math>t2 = d((ac)e + be) + d(ba + ca) + (db)a</math>

1. Menge der BPA-Terme definieren.
2. Zwei Terme aus BPA gegeben, und Prozessgraphen zeichnen.
3. Alle bisimilaren Knoten identifizieren.
4. Reduktionskalkül anwenden.
5. Sind sie bisimilar(Ja/Nein) Frage.
6. Ja/Nein Fragen zur Gewichtsfunktion.
   1. Wenn t-> t' reduziert werden kann , gilt dann gew(t) > gew(t')?
   2. Wenn t->* t' reduziert werden kann, gilt dann gew(t) > gew(t')?
   3. Wenn t=t' gilt dann dann gew(t)=gew(t')?
   4. Sind Prozessgraphen in BPA immer endlich?

Aufgabe 9

Noch eine Aufgabe zur Prozessalgebra.

1. Was für Dinge werden im BPA-Kalkül bewiesen? Bzw. um was dreht es sich im BPA-Kalkül. (Ja/Nein Fragen)
2. <math>t_1 + t_2</math>
   1. <math> t_1 \rightarrow t_2 </math>
   2. <math> t_1 \underline{\leftrightarrow} t_2 </math>
   3. <math> t_1 = t_2 </math>
3. Ist <math> t_1 \underline{\leftrightarrow} t_2 </math> entscheidbar?
4. Ist <math> \neg (t_1 \underline{\leftrightarrow} t_2) </math> entscheidbar?
5. Was bedeutet es, wenn das BPA-Kalkül korrekt ist?
6. Was bedeutet es, wenn das BPA-Kalkül vollständig ist?

Aufgabe 10

Folgender Harelgraph war gegeben: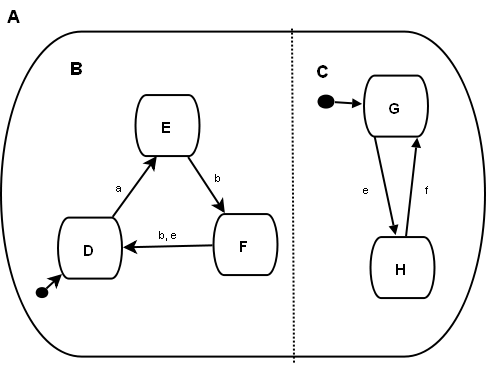

1. Male das Zustandsdiagram zu dem Harelgraphen.
2. Um was erweitern Harel-Graphen endliche Automaten?

Aufgabe 11

Aufgabe zum CTL-Modelchecking.

1. Beweisen sie, dass zu einer gegebenen CTL-Formel <math> \phi </math> der Model-Checking Algorithmus die Laufzeit O( <math>|\phi|*(|S|+|R|)</math>) hat.
2. Man musste die Formel EGa auf einer Kripkestruktur anwenden, und zeigen, wo sie gilt.

Aufgabe 12

DTM und RAM

6 Multiple Choice Fragen Komplexitaetsklassen von irgendwas (uniformes Mass und logarithmischens foo fuer Stellen und Plaetze)

Aufgabe 13

Vektorzeitstempel in eine vorhandene Struktur eintragen