Gedächtnisprotokoll FGI209-2
Zum zweiten Versuch der FGI2-Klausur wurde in PhilA geschrieben, Aufsichten hatten Herr Valk und Herr Köhler. Insgesamt waren 181Punkte zu erreichen, der Schwierigkeitsgrad war ähnlich hoch wie zur ersten Klausur.
Aufgabe 1
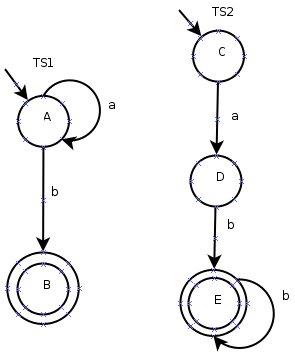
- Gegen waren zwei Transitionssysteme mit Sync = *leereMenge*. Geben sie das synchrone TS an.
- Geben sie L(TS_1) und L(TS_2) an, bestimmen sie auch L(TS_3) = L(TS_1) \cap L(TS_2)
- Formen sie TS_3 so um, dass es den Schnitt akzeptiert.
- Geben sie die Synchronisationsmenge an.
Aufgabe 2
Gegeben war ein (Workflow-)Netz <math>\mathcal N_1</math>, wo die letzte Stelle mit einer Transition mit der ersten verbunden war, sowie <math>\mathcal N</math>, wo diese Transition weggelassen wurde.
- Zeichnen sie den Erreichbarkeitsgraphen zu <math>\mathcal N_1</math>
- ...
- Geben sie drei Eigenschaften an, die ein Workflownetz ausmachen. Wahlweise formal oder informal.
- Wann ist ein Workflownetz korrekt?
- Ist diese Workflownetz korrekt?
- Ein paar Multiple-Choice Fragen (so oder so ähnlich)
- Ist <math>\mathcal N_1</math> k-beschränkt für <math>k=1</math>?
- Ist <math>\mathcal N_1</math> k-beschränkt für <math>k=2</math>?
- Ist <math>\mathcal N_1</math> reversibel?
- Ist <math>\mathcal N_1</math> lebendig?
Aufgabe 3
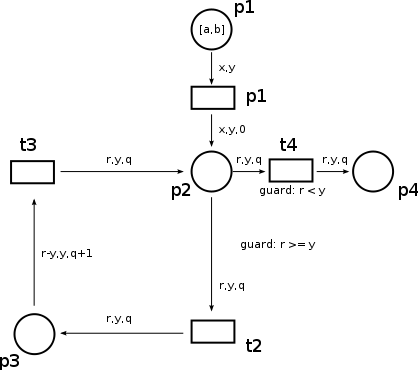
und eine Schaltsequenz <math>m_1 \rightarrow^{t_1} m_2 \rightarrow^{t_2} m_3 \rightarrow^{t_3} m_4 \rightarrow^{t_2} m_5 \rightarrow^{t_3} m_6 \rightarrow^{t_4} m_7</math> mit der Anfangsmarkierung a = 8, b = 2.
- Gebe die folgenden Markierungen an:
- <math>m_1(p_1) = \dots</math>
- <math>m_2(p_2) = \dots</math>
- <math>m_3(p_3) = \dots</math>
- <math>m_4(p_2) = \dots</math>
- <math>m_5(p_3) = \dots</math>
- <math>m_6(p_2) = \dots</math>
- <math>m_7(p_4) = \dots</math>
- Welche allgemeine Beziehung besteht auf <math>p_4</math> zwischen a, b, r, y, q?
- Ist das Netz k-beschrenkt für k=1? Begründe.
Aufgabe 4
Aufgabe 5
Gegeben war ein Lückentext-Baum, etwa so:
_ _ _ _ _ _ _ _
/ \
_ _ _ _ _ _ _ _
/ \ / \
_ _ _ _ _ _ _ _
der die Zwischenergebnisse eines bekannten Sortieralgorithmus aus der Vorlesung einzutragen waren. Es war eine Zeichenfolge, etwa 5 8 6 4 9 2 7 1, gegeben.
Außerdem gab es noch ein Paar Fragen
- Wann ist ein Algorithmus optimal?
- Ist dieser [Sortieralgorithmus] optimal?
- Wie ist die Zeitkomplexität dieses Algorithmus?
- Wie ist die Operatorenkomplexität des Algorithmus?
Aufgabe 6
Zwei BPA-Terme waren gegeben.
- Zeichnen sie die Prozessgraphen.
- Kennzeichnen sie die bisimilaren Knoten.
- Bestimmen sie die Normalformen mit den Regeln R1-R5.
- Sind die Terme bisimilar?
Aufgabe 7
Hier kam eine Aufgabe zum rekursiven Ableiten dran.
- Zeichnen sie den Prozessgraphen <X|E> mit {X=Ya+c, Y=Xc}.
- Leiten sie <X|E> mit für die Aktion a ab.
- Wann ist eine Spezifikation geschlossen?
- Ist diese Spezifikation geschützt?
Aufgabe 8
20 Punkte zu LTL und CTL
- Gegeben war eine Kripkestruktur. Geben sie alle PLätze an wo die Formel gilt.
- Wo liegen die Syntaktischen Unterschiede zwischen CTL und LTL?
- Geben sie je eine Formel an die für CTL oder LTL nicht korrekt ist.
- Geben sie Vor- und Nachteile von LTL- und CTL-Formeln an.
- ...
Aufgabe 9
Man musste die logischen, nicht die vektoriellen, Zeitstempel eintragen.
Aufgabe 10
- Wie unterscheiden sich der Ausfallalgorithmus von dem des byzantinischen Konsenses?
- Was ist Nachrichtenkomplexität?
- Geben Sie die Nachrichtenkomplexität des Ausfallalgorithmuses an.
- Warum ist der erste Algorithmus aus der Vorlesung exponentiell?
- Warum ist der zweite Algorithmus aus der Vorlesung polinomiell?