Gedächtnisprotokoll STO09-1: Unterschied zwischen den Versionen
SnuK (Diskussion | Beiträge) |
K (Bot: Kosmetische Änderungen) |
||
| (9 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Die Klausur von Herrn Drees fand am 28.07.2009 im Zeitraum von 9.00 bis 12.00 Uhr statt. Die Bearbeitungszeit war 120 Minuten. Als Hilfsmittel waren nur nicht-programmierbare Taschenrechner erlaubt. Skripte, Notizen oder Bücher waren nicht erlaubt. <br /> | |||
Die Klausur von Herrn Drees fand am 28.07.2009 im Zeitraum von 9.00 bis 12.00 Uhr statt. Die Bearbeitungszeit war 120 Minuten. Als Hilfsmittel waren nur nicht-programmierbare Taschenrechner erlaubt. Skripte, Notizen oder | Es gab insgesamt 80 Punkte zu erreichen. Zum Bestehen benötigt man 40 Punkte (Punkte der Teilaufgaben sind in Klammern angegeben). | ||
== Aufgabe 1) == | == Aufgabe 1) == | ||
Seien A, B, C drei Ereignisse in einem Wahrscheinlichkeitsraum, so dass P(A) = 0,6, <math>P(A \cap B \cap C) = 0,3</math> und <math>P((A \cup B) \setminus C) = 0,7</math> . Wie groß ist die Wahrscheinlichkeit <math>P(B \setminus A)</math> ? Begründen sie ihre Antwort! | Seien <math>A</math>, <math>B</math>, <math>C</math> drei Ereignisse in einem Wahrscheinlichkeitsraum, so dass <math>P(A) = 0,6</math>, <math>P(A \cap B \cap C) = 0,3</math> und <math>P((A \cup B) \setminus C) = 0,7</math> . Wie groß ist die Wahrscheinlichkeit <math>P(B \setminus A)</math> ? Begründen sie ihre Antwort! (8 Punkte) | ||
== Aufgabe 2) == | == Aufgabe 2) == | ||
Ein Würfel werde zwei mal geworfen. Sei A das Ereignis, dass im 1. Wurf eine Augenzahl von höchstens 3 fällt, B das Ereignis, dass die Summe der beiden Augenzahlen gerade ist. Berechnen sie die bedingte Wahrscheinlichkeit <math>P(A \ | Ein Würfel werde zwei mal geworfen. Sei <math>A</math> das Ereignis, dass im 1. Wurf eine Augenzahl von höchstens 3 fällt, <math>B</math> das Ereignis, dass die Summe der beiden Augenzahlen gerade ist. Berechnen sie die bedingte Wahrscheinlichkeit <math>P(A \mid B)</math>! Sind <math>A</math> und <math>B</math> stochastisch unabhängig? Begründen sie ihre Antwort! (12 Punkte) | ||
== Aufgabe 3) == | == Aufgabe 3) == | ||
Sei X eine <math>\lbrace 1, 2 \rbrace</math>- wertige Zufallsvariable und Y eine <math>\lbrace 3, 4 \rbrace</math>- wertige Zufallsvariable. In der nachfolgenden Tabelle sind die Wahrscheinlichkeiten | Sei <math>X</math> eine <math>\lbrace 1, 2 \rbrace</math>-wertige Zufallsvariable und <math>Y</math> eine <math>\lbrace 3, 4 \rbrace</math>-wertige Zufallsvariable. In der nachfolgenden Tabelle sind die Wahrscheinlichkeiten <math>P\lbrace X = x, Y = y \rbrace</math> gegeben. | ||
[[Bild:Sto tabular.png]] | |||
a) Bestimmen Sie die Zähldichte von <math>X</math> und <math>Y</math>. <br /> | |||
b) Sind <math>X</math> und <math>Y</math> stochastisch unabhängig? Begründen Sie! <br /> | |||
c) Berechnen Sie die Kovarianz von <math>X</math> und <math>Y</math>. <br /> | |||
(16 Punkte) | |||
== Aufgabe 4) == | == Aufgabe 4) == | ||
40 % aller Handyverträge werden von weiblichen Personen abgeschlossen, 60 % von männlichen Personen. Für eine Umfrage werden 100 Verträge rein zufällig ausgewählt. Geben Sei eine Approximation für die Wahrscheinlichkeit an, dass von den entsprechenden Vertragsinhabern mindestens 40 und höchstens 50 Personen weiblich sind! | 40% aller Handyverträge werden von weiblichen Personen abgeschlossen, 60% von männlichen Personen. Für eine Umfrage werden 100 Verträge rein zufällig ausgewählt. Geben Sei eine Approximation für die Wahrscheinlichkeit an, dass von den entsprechenden Vertragsinhabern mindestens 40 und höchstens 50 Personen weiblich sind! (8 Punkte) | ||
== Aufgabe 5) == | == Aufgabe 5) == | ||
Sei <math>f(x) = cx (1-x)1_{(0,1)}(x)</math> , <math>x \in \R</math> | Sei <math>f(x) = cx (1-x)1_{(0,1)}(x)</math> , <math>x \in \R</math> <br /> | ||
a) Wie ist c zu wählen damit f eine Dichte ist ? <br> | a) Wie ist <math>c</math> zu wählen, damit <math>f</math> eine Dichte ist? <br /> | ||
b) Sei X eine Zufallsvariable mit Dichte f. Berechnen sie E(X) und Var(X). <br> | b) Sei <math>X</math> eine Zufallsvariable mit Dichte <math>f</math>. Berechnen sie <math>E(X)</math> und <math>Var(X)</math>. <br /> | ||
c) Berechnen sie <math>P \lbrace \frac{1}{4} \leq X \leq \frac{3}{4} \rbrace</math>. Bestimmen | c) Berechnen sie <math>P \lbrace \frac{1}{4} \leq X \leq \frac{3}{4} \rbrace</math>. Bestimmen Sie dann mit Hilfe der Chebyshev'schen Ungleichung eine untere Schranke für diese Wahrscheinlichkeit. <br /> | ||
(16 Punkte) | |||
== Aufgabe 6) == | |||
= | Es werden <math>n</math> unabhängige, identisch verteilte Zufallsvariablen <math>X_{1}, ..., X_{n}</math> mit Verteilungsfunktion <math>F_{\vartheta } (x) = (1 - (\frac{x}{\vartheta})^{-2})1_{ [ \vartheta , \infty )}(x)</math>, <math>x \in \R</math> , beobachtet, wobei der Parameter <math>\vartheta > 0</math> unbekannt sei. | ||
a) Bestimmen Sie einen Maximum-Likelihood-Schätzer <math>\hat{\vartheta_{n}}</math> für <math>\vartheta</math> <br /> | |||
b) Zeigen sie, dass für den Maximum-Likelihood-Schätzer <math>\hat{\vartheta_{n}}</math> und alle <math>t \geq 1</math> gilt: <math>P \lbrace \frac{\hat{\vartheta_{n}}}{\vartheta} > t \rbrace = t^{-2n}</math>. Ist <math>\hat{\vartheta_{n}}</math> ein erwartungstreuer Schätzer? <br /> | |||
c) Verwenden Sie b) um zwei einseitige Konfidenzintervalle der Form <math>(0, T_{1}]</math> bzw. <math>[T_{2}, \infty )</math> jeweils zum Niveau <math>\alpha \in (0, 1)</math> für <math>\vartheta</math> zu konstruieren, wobei <math>T_{1}</math> und <math>T_{2}</math> geeignete von den Beobachtungen abhängige Zufallsvariablen sind. <br /> | |||
(20 Punkte) | |||
[[Kategorie:Gedaechtnisprotokoll|STO]] | |||
Aktuelle Version vom 8. Juni 2012, 17:09 Uhr
Die Klausur von Herrn Drees fand am 28.07.2009 im Zeitraum von 9.00 bis 12.00 Uhr statt. Die Bearbeitungszeit war 120 Minuten. Als Hilfsmittel waren nur nicht-programmierbare Taschenrechner erlaubt. Skripte, Notizen oder Bücher waren nicht erlaubt.
Es gab insgesamt 80 Punkte zu erreichen. Zum Bestehen benötigt man 40 Punkte (Punkte der Teilaufgaben sind in Klammern angegeben).
Aufgabe 1)[Bearbeiten]
Seien <math>A</math>, <math>B</math>, <math>C</math> drei Ereignisse in einem Wahrscheinlichkeitsraum, so dass <math>P(A) = 0,6</math>, <math>P(A \cap B \cap C) = 0,3</math> und <math>P((A \cup B) \setminus C) = 0,7</math> . Wie groß ist die Wahrscheinlichkeit <math>P(B \setminus A)</math> ? Begründen sie ihre Antwort! (8 Punkte)
Aufgabe 2)[Bearbeiten]
Ein Würfel werde zwei mal geworfen. Sei <math>A</math> das Ereignis, dass im 1. Wurf eine Augenzahl von höchstens 3 fällt, <math>B</math> das Ereignis, dass die Summe der beiden Augenzahlen gerade ist. Berechnen sie die bedingte Wahrscheinlichkeit <math>P(A \mid B)</math>! Sind <math>A</math> und <math>B</math> stochastisch unabhängig? Begründen sie ihre Antwort! (12 Punkte)
Aufgabe 3)[Bearbeiten]
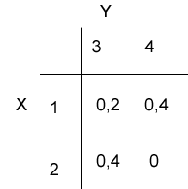
Sei <math>X</math> eine <math>\lbrace 1, 2 \rbrace</math>-wertige Zufallsvariable und <math>Y</math> eine <math>\lbrace 3, 4 \rbrace</math>-wertige Zufallsvariable. In der nachfolgenden Tabelle sind die Wahrscheinlichkeiten <math>P\lbrace X = x, Y = y \rbrace</math> gegeben.
a) Bestimmen Sie die Zähldichte von <math>X</math> und <math>Y</math>.
b) Sind <math>X</math> und <math>Y</math> stochastisch unabhängig? Begründen Sie!
c) Berechnen Sie die Kovarianz von <math>X</math> und <math>Y</math>.
(16 Punkte)
Aufgabe 4)[Bearbeiten]
40% aller Handyverträge werden von weiblichen Personen abgeschlossen, 60% von männlichen Personen. Für eine Umfrage werden 100 Verträge rein zufällig ausgewählt. Geben Sei eine Approximation für die Wahrscheinlichkeit an, dass von den entsprechenden Vertragsinhabern mindestens 40 und höchstens 50 Personen weiblich sind! (8 Punkte)
Aufgabe 5)[Bearbeiten]
Sei <math>f(x) = cx (1-x)1_{(0,1)}(x)</math> , <math>x \in \R</math>
a) Wie ist <math>c</math> zu wählen, damit <math>f</math> eine Dichte ist?
b) Sei <math>X</math> eine Zufallsvariable mit Dichte <math>f</math>. Berechnen sie <math>E(X)</math> und <math>Var(X)</math>.
c) Berechnen sie <math>P \lbrace \frac{1}{4} \leq X \leq \frac{3}{4} \rbrace</math>. Bestimmen Sie dann mit Hilfe der Chebyshev'schen Ungleichung eine untere Schranke für diese Wahrscheinlichkeit.
(16 Punkte)
Aufgabe 6)[Bearbeiten]
Es werden <math>n</math> unabhängige, identisch verteilte Zufallsvariablen <math>X_{1}, ..., X_{n}</math> mit Verteilungsfunktion <math>F_{\vartheta } (x) = (1 - (\frac{x}{\vartheta})^{-2})1_{ [ \vartheta , \infty )}(x)</math>, <math>x \in \R</math> , beobachtet, wobei der Parameter <math>\vartheta > 0</math> unbekannt sei.
a) Bestimmen Sie einen Maximum-Likelihood-Schätzer <math>\hat{\vartheta_{n}}</math> für <math>\vartheta</math>
b) Zeigen sie, dass für den Maximum-Likelihood-Schätzer <math>\hat{\vartheta_{n}}</math> und alle <math>t \geq 1</math> gilt: <math>P \lbrace \frac{\hat{\vartheta_{n}}}{\vartheta} > t \rbrace = t^{-2n}</math>. Ist <math>\hat{\vartheta_{n}}</math> ein erwartungstreuer Schätzer?
c) Verwenden Sie b) um zwei einseitige Konfidenzintervalle der Form <math>(0, T_{1}]</math> bzw. <math>[T_{2}, \infty )</math> jeweils zum Niveau <math>\alpha \in (0, 1)</math> für <math>\vartheta</math> zu konstruieren, wobei <math>T_{1}</math> und <math>T_{2}</math> geeignete von den Beobachtungen abhängige Zufallsvariablen sind.
(20 Punkte)