PRODUCT NETS
Product Nets result from augmenting Petri Nets with inhibitor arcs and erase arcs by arc labels, transition inscriptions and individual tokens.
Definition
A Product Net consists of
- a preamble in which the used sets and functions are defined
- an unlabelled net with a set of places S, a set of transitions T and a set of arcs comprising inhibitor arcs and erase arcs
- a labelling with
- arc labels for each arc, which are n-tuples of terms which may be preceded by multiplicities
- transition inscriptions (optional), which are predicates in the bound variables of the transition
- domains for places (define the tokens that may be present at the places), which are products of sets or subsets of products
Marking
A Marking M of a Product Net is a family of mappings, each one placing (one or more) specific elements of the appropriate domain at each place of the net.
Interpretation
An interpretation is an assignment to each variable x of a value from a specific range of values.
A permissable interpretation of the bound variables of a transition t is an interpretation which satisfies:
- Bound variables are assigned only natural numbers or those values that are elements of the sets defined in the preamble.
- Interpretations of the bound variables of a transition t are extendable to all terms which appear in the input and output arc labels and, possibly, in the transition inscriptions.
- The extension of the interpretation over labels of the input and output arcs must result in markings according to the domain of the respective place.
Each permissible interpretation of the bound variable of a transition t is assigned a threshold marking, which is defined through the extension of the interpretation onto the labels of the input arcs.
Transition Rule
A transition t is enabled under a marking M and by a permissible interpretation of its bound variables if the following holds:
- At the input places of t there must be at least the tokens of the threashold marking.
- The transition inscription - if present - must be true under the given interpretation.
- No token from the respective inhibitor set may reside at the inhibitor places of t.
The occurrence of the transition t generates the successor marking, which can be described in three steps:
- The marking of the input places is reduced by the marking which is described by the extension of the interpretation of t over the labels of the respective input arcs; i.e., the marking is decremented by the threshold marking.
- All tokens that are elements of the respective erase sets are removed from the erase places.
- The marking of the output places is increased by the marking which is described by the extension of the interpretation of t over the respective output arcs.
Sample Net
Preamble:
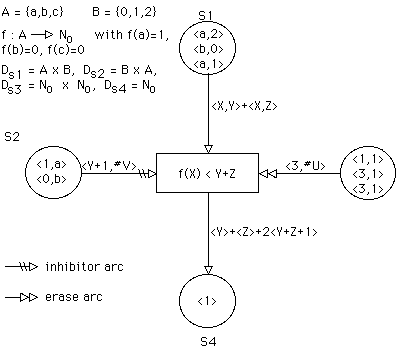
X, Y and Z are bound variables of the transition, and #U and #V are free variables.
Tools
The Product Net Machine is an integrated tool for the specification and the analysis of Product Nets.
References
H. J. Burkhardt, P. Ochsenschläger, R. Prinoth: Product Nets - A formal description technique for cooperating systems [bop89]
BACK
